FZF, the fuzzy command-line finder, is a really useful small tool for your command line that makes it easier to 1. quickly search your shell’s command history, 2. quickly find+select files/folders to pass to a command, and 3. quickly find a directory and change into it.
Tag: search
Yet another small number-equation-puzzle with a solver in Prolog
This post is about yet another small number puzzle, and the corresponding solver for it in Prolog. The post and code is written to be easily understandable and help learn the basics of "think and code" in Prolog.
Einstein Riddle/Zebra Puzzle in Prolog
In this post we solve another logic puzzle deriving rules from the puzzle and stating them in Prolog. And this time it is a rather famous puzzle one: the Zebra puzzle (also called Einstein riddle/puzzle).
Solving Logic Puzzles in Prolog: Puzzle 3 of 3
There are four researchers: Ainsley, Madeline, Sophie and Theodore. The goal is to find out their sports competition discipline, birth year and research interests (while knowing that each of the mentioned attributes is different amongst them). In order so solve the puzzle, a couple of hints is provided from which the solution can be derived.
Solving Logic Puzzles in Prolog: Puzzle 2 of 3
Eilen, Ada, Verena and Jenny participated in a painting competition. Find out who painted which subject and who took which place in the competition, using the hints provided.
Solving Logic Puzzles in Prolog: Puzzle 1 of 3
There are 4 students: Carrie, Erma, Ora und Tracy. Each has one scholarship and one major subject they study. The goal is to find out which student has which scholarship and studies which subject (with all scholarships and majors being different from each other) from the hints provided.
Hidoku Solver in Python: branch cutting, intelligent successor generation and some simplifications
In this post we are implementing a Hidoku solver (Hidoku is yet another fine number puzzle) that uses a depth first search, branch cutting, limited (intelligent) successor generation and some automatic simplification. Usually, a Hidoku is a quadratic board consisting of n x n fields - but rectangular or other forms would be possible as well. With each Hidoku, some fields are already pre-filled with numbers at the beginning. The game goal is to fill in all other numbers so that an ascending number queue is built: each number has to be adjacent to it's successor, with adjacent meaning in an adjacent horizontal, vertical or diagonal field.
Draught board puzzle / checkerboard puzzle solver in Python
The checkerboard puzzle or draught board puzzle (also called Krazee Checkerboard Puzzle, Banzee Island checkerboard puzzle, Zebas puzzle, etc.) is a mutilated chessboard problem, which further is a tiling puzzle/dissection puzzle. Hence, the core problem is similar to the one of solving the well known Tangram, which some of you might be familiar with. The … Continue reading Draught board puzzle / checkerboard puzzle solver in Python
Magic number board puzzle solver in Python
The magic number board puzzle is yet another equation puzzle (similar to the first equation puzzle or Jodici) - but has a notable larger solution space. The magic number board is a quadratic board, consisting of 5x5 = 25 fields, which are organized as 5 horizontal rows and 5 vertical columns. Each field should contain … Continue reading Magic number board puzzle solver in Python
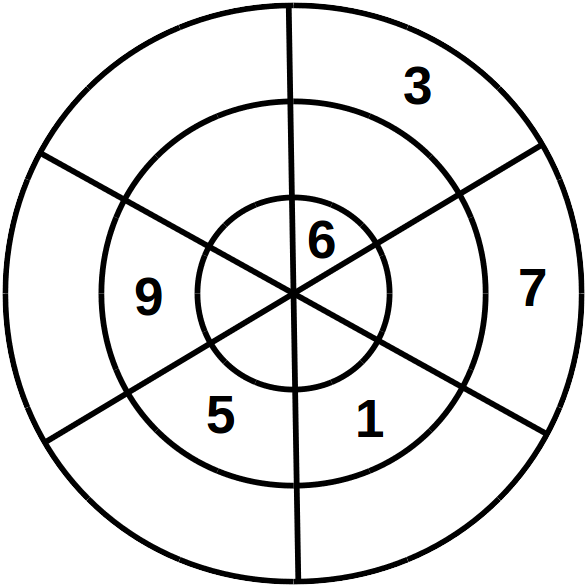
Jodici solver: Python vs Prolog
Jodici is a fun and intuitive number placement puzzle. It consists of a circle which a) contains 3 nested rings and b) is divided into 6 cake-piece-like sectors. As with Sudoku, the goal is to fill in all numbers, while satisfying certain rules: each field must contain an integer [1,9], with each such integer being used twice in total. Further, each sector sums up to 15 and each ring to 30.